さくらんぼ計算の教え方が難しいと悩んでいる親御さんは結構いますよね。
そもそも、さくらんぼ計算って何?と思って教え方より前に自分が調べなくてはいけない人も多いはずです。
さくらんぼ計算の教え方は簡単ですが、簡単な問題だとなんでやる必要があるのかわからない子もいます。
なので、混乱してしまいなかなか覚えられないという子もいるでしょう。
そこで今回はさくらんぼ計算の教え方を足し算・引き算・掛け算・割り算それぞれで紹介します。
早いうちに足し算・引き算・掛け算・割り算のさくらんぼ計算を覚えられれば、暗算もやりやすくなるので計算が速くなるでしょう。
また二桁の計算が苦手な子も多いので、そういう子はゆっくりさくらんぼ計算で訓練すると算数への苦手意識が減る子もいます。
二桁になると一気に面倒くさくなるので、算数が嫌!という子も少なくないです。
なので、さくらんぼ計算で二桁の計算への苦手意識がなくなるとありがたいと思いませんか?
まずは、さくらんぼ計算の教え方をマスターしてくださいね。
さくらんぼ計算の教え方のコツ 二桁の計算にもおすすめ
さくらんぼ計算の教え方が難しいと感じる親御さんも多いですが、一度覚えてしまえば子供はどんどん回答が速くなります。
なので、早いうちにさくらんぼ計算を覚えておくと二桁の計算も楽になっていいです。
さくらんぼ計算の教え方のコツはまずどんな計算方法で、そのメリットを教えること。
なぜさくらんぼ計算を覚えた方がいいのかわからなければ、やる気が起きません。
できるだけ簡単に速く答えを導き出せることを教えてあげましょう。
10以上の二桁の答えになる場合、計算が苦手な子は以下のところでつまずきます。
なので、二桁の計算が苦手な子にはさくらんぼ計算を教えることでメリットが大きいんです。
-
- 二桁だと手で数えることができない
計算が苦手な1年生の子はそもそも頭の中で計算していません。
たいていの場合、手で数えたり物を使って足したり引いたりしています。
自宅では物を使うこともできますが、学校ではそうはいきませんよね?
なので、どうしても10以上の答えを導き出す場合、指の数が足りないので計算が困難になります。
だからこそ、さくらんぼ計算を使えれば計算が速くなれると教えてあげましょう!
-
- 二桁だと紙に図を描くのが大変で時間がかかる
指を使えない10以上の数であれば、紙に描けばいいじゃん!と思うかもしれません。
でも、こんなことをいちいち1つずつやっていたら終わりませんよね。
だからこそ、さくらんぼ計算を使えば、ずっと速く答えがわかるんだよと教えてあげましょう。
ぶっちゃけさくらんぼ計算も「さくらんぼの絵」の中に数字を入れるので、絵を描くじゃん!と思いますよね。
でも、このさくらんぼに二桁の数字を入れるだけでパッと計算できるなら速さ・正確さに差が出るんです。
さくらんぼ計算の目的は二桁の数字など大きくなっても、視覚的にパッとわかりやすく計算すること。
どちらかの数字を10や20など最後が0になる数字にしてしまうのが一番わかりやすいです。
10の数に足すだけなら後の数字を0に当てはめればいいだけですよね?
なので、さくらんぼ計算では10や20など、最後が0になるように前の数字をすっきりさせることを考えます。
また、さくらんぼ計算の教え方のコツは最初のうちは単純なものからスタートするのがおすすめ。
大きい数だとわかりづらいので、最初は小さい数・足し算から始めましょう。
もし、さくらんぼ計算を教えてもなかなか理解していない場合は、そろばんを習っている子・計算の回答を暗記してしまっている可能性があります。
答えを暗記している子は学年が上がってからつまずく可能性があるので、さくらんぼ計算の前に数を量ととらえられるように家で練習しましょう。
例えば…
-
- おやつ○○個渡し、兄弟でわける
- スーパーでお小遣いを渡して自分で計算して買い物する(簡単なお菓子でOK)
数の増減について学べるので、最初は難しくても親子で一緒にやってみましょう。
さくらんぼ計算の教え方:足し算
さくらんぼ計算の教え方のコツは足し算からスタートするとわかりやすいです。
答えが二桁になると一気に苦手になる子もいるので、二桁の答えになるものでも簡単なものから始めましょう。
さくらんぼ計算では足される数と足す数があったら、足す数の方を2つの数字に分解して前の数を10や1の位を0にして計算しやすくする方法です。
例:8+5=13の場合
8+5=13の場合、前の8はいくつ足したら10になるのか考えます。
2を足せば10になりますよね?
それでは後から足す5を分解するとどうなるでしょうか?
2を前の8に足したいのですから5=2と3に分解します。
つまり、8+(2+3)という式になります。
※カッコの中の2+3が後ろの5の部分です。
8+2=10+3になり、さらに10+3=13と答えが出ます。

それではもう少し大きい数で試してみましょう。
例:37+25の場合
こちらも前述の計算と同じようにまずは前の37に注目し、40になるように考えます。
37を40にするには3を足せばいいですよね?
なので、まずは後ろの25を3と22に分けます。
37+3=40+22(25から3を引いた残りの数)にします。
40+22=62はすぐに出てきますよね。

まあ、大人からしたらちょっと面倒と思うかもしれません。
でも、小学一年生くらいの子供だと10以上の足し算でも時間がかかる子がいます。
また、大人も無意識に数字を分解して暗算しているので、さくらんぼ計算が役に立つんです。
さくらんぼ計算の教え方:引き算
今度は引き算のさくらんぼ計算の教え方になりますが、こちらも基本的な考え方は足し算と一緒です。
前の二桁の数を10にすることを考えて後ろの数字を分割します。
例:14-6=8の場合
14-6=8の場合、前の数を10にするにはいくつ引けばいいのか考えます。
シンプルに1の位の数字を見ればわかるので、4を引けばいいですよね?
それでは後から引く6を分解するとどうなるでしょうか?
4を前の14から引きたいのですから6=4と2に分解します。
つまり、14-4-2という式になります。
※-4と-2が後ろの6の数字を分解した部分です。
14-4=10-2になり、さらに10-2=8と答えが出ます。
それでは今度はもう少し大きい二桁の数字にしていましょう。
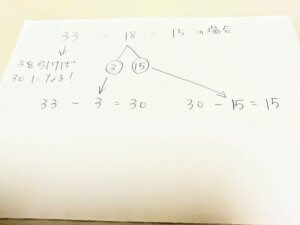
例:33-18の場合
まずは33の後ろの部分を0(30)にするにはいくつ引けばいいのか考えます。
33を30にするには3を引きますよね。
なので、18を3と15に分解してください。
33-3=30-15になります。
ここでスパッと30から15を引くことができない場合はさらにさくらんぼ計算してみましょう。
後ろの15を10と5に分けて、30から10引きます。
30-10=20になり、残りの5を引けば15と出てきます。
引くのが難しい場合はどんどん数を分解してさくらんぼ計算にしていきましょう。
ただし、大きい数を計算するころにはひっ算を使うと思います。
あくまでもさくらんぼ計算は暗算や計算の仕方をスムーズに頭でもできるようにするのに力を発揮するものです。
さくらんぼ計算の教え方:掛け算
掛け算はぶっちゃけひっ算の方が早いです。
さくらんぼ計算だと回答を出すまでの工程が長いので、ひっ算ができるなら二桁の数字のひっ算の方がいいでしょう。
ただし、二桁のひっ算の掛け算が苦手で足し算の方が間違えにくいという子はさくらんぼ計算を活用してください。
例:13×15の場合
まず、それぞれの数を分解していきます。
13は10と3、15は10と5に分解して、前の10と後ろの10を掛けます。
前の10と後ろの5、前の3と10、前の3と5を掛けます。
10×10=100
10×5=50
3×10=30
3×5=15
これをすべて足します。
100+50+30+15=195

ひっ算で掛け算でやっていることと同じですが、繰り上がりがあると間違いやすい子もいます。
なので、二桁のひっ算で間違いやすい子はこちらのさくらんぼ計算で答えを導き出せる方法を使うのも手ですよ。
さくらんぼ計算の教え方:割り算
二桁など大きな数の割り算の場合、ひっ算を使えば速いと思うかもしれません。
しかし、ひっ算でも大きな数で割る数が一番左の数よりも大きい場合はもたもたします。
なので、割り算でもさくらんぼ計算を使う癖をつけておくと便利です。
前もって親御さんも割り算のさくらんぼ計算の教え方を覚えておくことをおすすめします。
あまりのない割り算・あまりのある割り算があるので、それぞれ教え方が異なるので別々に見てみましょう。
さくらんぼ計算の教え方:あまりのない割り算
あまりのない割り算の場合はシンプルなので、さくらんぼ計算の教え方も簡単です。
さくらんぼ計算の教え方はざっくり大きく割ることを考えるようにするのがコツ。
例:96÷4の場合
まず、前の二桁の数字・96を90と6に分けます。
6はそのままいったん放置して、90を4で割る形にします。
ただし、細かいところまで割るのではありません。
90ではなく9を4で割るつもりで計算してください。
9÷4=2あまり1になるので、それぞれの最後に0を加え桁数を戻します。
つまり、90÷4=20あまり10の形。
次に余った10に最初放置した6を足します。
10+6=16を4で割ってください。
16÷4=4になります。
前述で計算した20に4を足して、答えは24になります。

または96を80と16に分解して4で割ってもOK。
すると80÷4=20
16÷4=4
答えは24になり、こちらの方がわかりやすいかもしれません。
わかりやすい方で回答してください。
さくらんぼ計算の教え方:あまりのある割り算
あまりのある割り算の場合もそこまで面倒ではないので、覚えておくと確認作業で活用しやすいです。
コツは割られる数で一番大きいものはいくつかと考えること。
例:47÷5の場合
まず、5で割れる一番大きい数字に分けます。
※基本的に九九をマスターしていないと厳しいです。
47を45と2に分けます。
45÷5=9
2は5で割り切れないので、あまり2になります。

九九がまだしっかりできていない子はわかりやすい40で計算するかもしれません。
でも、まだ7の中にはまだ5が隠れていますよね?
47に隠れている5の一番大きい数字を考える必要があります。
常に割られる数字の中に隠れている一番大きな数字を導き出す訓練をするとひっ算で割り算を考える上でも早くなります。
実際にうちの子供も最初のころ、ひっ算を使った割り算で苦労していたんです。
例えば、495÷5などは一番左の数字「4」のみを5で割ることはできませんよね?
つまり、49を5で割る必要があるんです。
なので、さくらんぼ計算で49を分解するとパッと計算しやすくなります。
ひっ算を使う上でもさくらんぼ計算の癖がついていれば、頭の中でパッと数を分解できるんです。
さくらんぼ計算の教え方:小数点以下のある数の割り算
さくらんぼ計算を使わないと結構計算が面倒なのが、小数点以下のある数の割り算です。
さくらんぼ計算の教え方は普通の割り算とほとんど変わらないですが、「0.」を戻すのを忘れないようにするのがポイントです。
例:6.9÷3の場合
まず、6.9を6と0.9に分けます。
0.9はそのままいったん放置して、6を3で割ります。
6÷3=2
残っている0.9を今度は3で割りますが、いったん前の0を取って考えるとわかりやすいでしょう。
9÷3=3になるので、前に0つけ0.3に戻します。
前jつで計算した2に0.3を足して、答えは2.3になります。

基本的に複雑になるものはひっ算を使った方が早いでしょう。
あくまでも解法の一つと考えてください。
さくらんぼ計算の教え方は最初は難しいものの、一度覚えてしまえば簡単なのでじっくり何度も問題を解かせてください。
まずは簡単な問題からスタートすれば、やり方をマスターしやすいので試してみましょう。
今後、計算問題を解く上でも簡単にできるようになると思いますよ。